○鑑定コラム
フレーム表示されていない場合はこちらへ
トップページ
田原都市鑑定の最新の鑑定コラムへはトップページへ
前のページへ
次のページへ
鑑定コラム全目次へ
「新規賃料の積算賃料と比準賃料の賃料額の関係について」
不動産鑑定士
桐蔭横浜大学法学部客員教授
田原 拓治
1.はじめに
店舗の家賃訴訟に関係して、一つの賃料鑑定書を見ることになったが、その鑑定書の新規賃料(正常実質賃料)の積算賃料と比準賃料との間に、2.5倍近く(積算賃料月額489,800円、比準賃料月額197,100円)の開きがあった。積算賃料と比準賃料との賃料額の関係について、下記で考察する。
2.正常実質賃料
正常実質賃料とは、正常賃料の実質賃料をいう。
① 正常賃料
正常賃料とはどういう賃料かと云えば、不動産鑑定評価基準(以下「鑑定基準」と呼ぶ)は、次のごとく規程する。
「正常賃料とは、正常価格と同一の市場概念の下において新たな賃貸借等(賃借権若しくは地上権又は地役権に基づき、不動産を使用し、又は収益することをいう。)の契約において成立するであろう経済価値を表示する適正な賃料(新規賃料)をいう。」(平成26年改正鑑定基準 国交省版P17)
正常賃料とは、現実の社会経済情勢の下で合理的と考えられる条件を満たす不動産賃貸市場で形成されるであろう市場価値を表示する適正な新規賃料を云う。
② 実質賃料と支払賃料
実質賃料とは、賃料の内容による区分される賃料で、支払賃料に対応する賃料であり、鑑定基準は、次のごとく規定する。
「実質賃料とは、賃料の種類の如何を問わず賃貸人等に支払われる賃料の算定の期間に対応する適正なすべての経済的対価をいい、純賃料及び不動産の賃貸借等を継続するために通常必要とされる諸経費等(以下「必要諸経費等」という。)から成り立つものである。」(平成26年改正鑑定基準 国交省版P31)
賃借人が不動産を借りていることに伴って、当該不動産の所有者の賃貸人に対して支払う適正な全ての経済的対価が実質賃料である。
実質賃料を構成するものは、下記である。
・支払賃料
・共益費
・敷金・保証金の運用益
・礼金の償却額
・保証金のうち償却される部分
・更新料の賃借期間償却額
実質賃料に対応して区分される支払賃料とは、鑑定基準は、下記のごとく述べる。
「支払賃料とは、各支払時期に支払われる賃料を云う」。(平成26年改正鑑定基準 国交省版P31)
③ 正常実質賃料
正常実質賃料とは、上記の考察より、現実の社会経済情勢の下で合理的と考えられる条件を満たす不動産賃貸市場で形成されるであろう市場価値を表示する適正な賃料であり、賃借人が賃貸人に支払う支払賃料、共益費、 敷金・保証金の運用益、礼金の償却額、保証金のうち償却される部分、更新料の賃借期間償却額を合計した賃料ということになる。
3.3つの価格及び賃料
不動産の価格及び賃料分析は、不動産の所有する特性から、3つの側面から検討、分析されて求められる。
一つは、不動産を形成、構成する原価(コスト)の面からの分析で、求める方式を原価方式と呼び、手法を価格では原価法と呼ぶ。求められる価格を積算価格と呼ぶ。賃料での手法は積算法と呼び、求められる賃料を積算賃料と呼ぶ。
二つは、不動産の市場性を反映する分析で、求める方式を比較方式と呼び、手法を価格では取引事例比較法と呼び、求められる価格を比準価格と呼ぶ。賃料での手法は賃貸事例比較法と呼び、求められる賃料を比準賃料と呼ぶ。
三つは、不動産が生み出す収益からの分析で、求める方式を収益方式と呼び、手法を価格では収益還元法と呼ぶ。求められる価格を収益価格と呼ぶ。賃料での手法は収益分析法と呼ぶ。求められる賃料を収益賃料と呼ぶ。
賃料の収益賃料は、事業の売上高より原価、販売管理費を控除して純収益を求め、その純収益の中の不動産に帰属する収益を求め、それに必要諸経費を加算して求める。
この収益分析法は、売上高が事業経営者の経営力に影響される面が多く,かつ不動産に帰属する純収益の把握が難しいため、一般的にはあまり行われていない。
4.3つの価格及び賃料の等価性について
3つの価格及び賃料の金額については、理論上は一致すると云われている。
① 門脇惇説
不動産鑑定評価は、不動産が具有するそれぞれの面からの分析価格として、コストの面より積算価格、市場性の面より比準価格、収益性の面より収益価格の価格がある。
そして、3つの価格は理論上は一致すると云われている。
そのことについては門脇惇氏が著書『不動産鑑定評価要説』P120(税務経理協会、昭和46年)で次のごとく述べられている。
「3試算価格は、それぞれ、効用に見合う面、造る費用を償う面、一般に認められてその価格で取引される面、すなわち価格の三面性に照応するものであり、市場で揉まれ、淘汰されて、一つの正常価格に帰一するものであると解すべきこと。」(資料10 省略)
② 武田公夫説
また武田公夫氏は、著書『不動産評価の知識』P133(日本経済新聞社、1993年)で、次のごとく述べられている。
「各方式の適用によって求められた試算価格または試算賃料は、理論的には一致するはず」
と3価格及び賃料の理論的一致を認める。(資料11 省略)
実際には一致しないが、それは「資料不足など」によるのが原因でありと述べられる。
5.積算賃料と比準賃料が使用される局面
継続賃料を求める場合、いきなり継続賃料を求められるものでは無い。上記不動産の具有する特性から、3つの側面からの検討、分析が行われる。
前記したごとく、賃料評価の場合、事業売上高からの収益分析は行われることが少なく、殆どが積算法と賃貸事例比較法である事から、論もその2手法の賃料を前提に進める。
継続賃料の求める過程を述べると、最初に新規賃料を求める。その新規賃料を使用して、継続賃料評価の手法である差額配分法を求める。そして利回り法、スライド法、継続賃料の賃貸事例比較法を行い、各手法の試算賃料を求めて、試算賃料の調整と決定を行って、継続賃料を決定する。
積算賃料と比準賃料が使用される局面は、新規賃料(正常実質賃料)を求める個所のところである。それも差額配分法の継続賃料を求める為に求めるのである。
それ故、差額配分法の賃料が4つの手法の試算賃料の中で最も重要視されることになる。
6.不動産鑑定士実務修習テキストの積算賃料と比準賃料
① 不動産鑑定士試験と実務修習
不動産鑑定士になるには短答試験と論文試験に合格し、合格後実務修習があり、実務修習の講義、演習を経て、小論文、口頭試問の試験に受かって、不動産鑑定士の登録がなされる。
実務修習に使用される「実務修習・指導要領テキスト」には、類型別に不動産鑑定書のモデルが取り上げられて、記載されている。そのモデル例題は、不動産鑑定士になって業務を行う場合に多く利用されている。
② 実務修習テキストの新規賃料の積算賃料と比準賃料
「実務修習・指導要領テキスト」は、毎年改訂されるものでは無い。
私の手許には、毎年の「実務修習・指導要領テキスト」があるわけでは無い。第11回実務修習テキスト(編集公益社団法人日本不動産鑑定士協会連合会 2016年1月1日発行)がある。そのP244に「新規・継続家賃の鑑定評価(評価書編)」がある。
RC造9階建の店舗・事務所ビルの1階店舗300㎡の賃料を求める鑑定書のモデルである。
ビル1棟(延べ床面積5,430㎡)の新規賃料(正常実質賃料)が積算賃料と比準賃料とで求められている。(同書P263 資料12 省略)
積算賃料、比準賃料は、下記である。
積算賃料 月額 4,520,000円
比準賃料 月額 4,500,000円
積算賃料の金額を1.0とすると、比準賃料の割合は、
4,500,000円
────────= 0.9955≒0.996
4,520,000円
0.996である。
積算賃料と比準賃料の開差は非常に小さい。
7.判例に見る新規賃料の積算賃料と比準賃料
① 判例の新規賃料の積算賃料と比準賃料
毎年多くの賃料増減額請求事件が日本全国の裁判所で審議、判決されている。
多くは和解で終わるものが多いが、判決に至る案件もある。
その判決の中で、新規賃料を積算賃料のみで行っている場合もある。また積算賃料と比準賃料が求められて新規賃料を決定している場合でも、積算賃料、比準賃料の金額が記述されていない判決もかなり多い。
裁判所鑑定人不動産鑑定士の鑑定(注)によったもので、積算賃料、比準賃料の金額明示の判決例を捜した。
とても全賃料増減額請求事件の判決を見ることは出来ない。私の出来る範囲で入手した判決事例である。下記一覧の9判例、12事例である。
東京地裁、東京高裁の判例を選んだわけでは無いが、結果として東京地裁、東京高裁の判例となってしまった。
採用判例は、資料番号1~9として、最後にコピー添付するが、判決表題部ページと当該賃料部分が掲載されているページのみとする。(資料1~9 省略)
(注)資料4は、一審判決では、鑑定人の鑑定賃料を採用していたが、2審の東京高裁判決は、被告側提出の鑑定書の新規賃料を採用しているため、その新規賃料を採用する。
|
資料番号
|
裁判所
|
判決年月
|
出典
|
事件番号
|
階
|
月額積算賃料 万円
|
月額比準賃料 万円
|
比準賃料/積算賃料
|
|
1
|
東京地裁
|
平成4年3月16日
|
判例タイムズ811-223
|
平2(ワ)第141637号
|
|
23.65
|
19.87
|
0.840
|
|
2
|
東京地裁
|
平成10年10月7日
|
判例タイムズ1020-208
|
平10(ワ第2742号
|
|
82.70
|
83.20
|
1.006
|
|
3
|
東京高裁
|
平成13年10月29日
|
判例時報1765-49
|
平13(ネ)第1962・3036号
|
|
4350.10
|
3924.20
|
0.902
|
|
4
|
東京高裁
|
平成16年1月15日
|
インターネット
|
平15(ネ)第1754号
|
|
12598.70
|
12541.80
|
0.995
|
|
5
|
東京地裁
|
平成17年3月25日
|
判例タイムズ1219-346
|
平15(ワ)第2526号
|
|
6460.00
|
6489.00
|
1.004
|
|
6-1
|
東京高裁
|
平成18年11月30日
|
判例タイムズ1257-314
|
平18(ネ)第2098号
|
地下1階
|
127.62
|
130.07
|
1.019
|
|
6-2
|
東京高裁
|
平成18年11月30日
|
判例タイムズ1257-314
|
平18(ネ)第2098号
|
1階
|
212.23
|
216.10
|
1.018
|
|
6-3
|
東京高裁
|
平成18年11月30日
|
判例タイムズ1257-314
|
平18(ネ)第2098号
|
2階
|
12.00
|
12.04
|
1.003
|
|
9-4
|
東京高裁
|
平成18年11月30日
|
判例タイムズ1257-314
|
平18(ネ)第2098号
|
4階
|
21.07
|
18.04
|
0.856
|
|
7
|
東京地裁
|
令和2年6月23日
|
第一法規データペース
|
平30(ワ)第34480号
|
|
87.68
|
73.30
|
0.836
|
|
8
|
東京地裁
|
令和2年10月9日
|
第一法規データペース
|
平31(ワ)第10732号
|
|
43.70
|
42.10
|
0.963
|
|
9
|
東京地裁
|
令和3年1月15日
|
第一法規データペース
|
平31(ワ)第6184号
|
|
3340.00
|
3520.00
|
1.054
|
|
平均
|
|
|
|
|
|
|
|
0.958
|
|
標準偏差
|
|
|
|
|
|
|
|
0.078
|
|
変動係数
|
|
|
|
|
|
|
|
0.081
|
② 分析結果
鑑定基準は、差額配分法に採用する新規賃料を求めるについては、次のごとく述べる。
「対象不動産の経済価値に即応した適正な実質賃料は、価格時点において想定される新規賃料であり、積算法、賃貸事例比較法等により求めるものとする。」(平成26年改正鑑定基準国交省版P34)
積算賃料を1.0として、比準賃料の割合を求める。
比準賃料
──────────
積算賃料
の割合である。
求められた比準賃料/積算賃料の割合を区分表示すると下記である。
割合 データ数
1.010以上 3
1.0~1.01未満 3
0.95~1.0未満 2
0.90~0.95未満 1
0.85~0.90未満 1
0.80~0.85未満 2
計 12データ
データの倍率は、0.836~1.054の間にある。
上記9判例、12事例の積算賃料に対する比準賃料の平均割合は、0.958、標準偏差0.078である。
これは、
積算賃料 100
比準賃料 95.8
ということである。
先に3つの価格・賃料は等価になると延べた。そしてそれは理論上であって、実際には等価にならないと記した。
現実の裁判判例に残された賃料結果を見れば、積算賃料100とすると、比準賃料は95.8である。その開差より考察すれば、3つの価格・賃料は等価になるという考え方は妥当であると判断される。
③ 自然現象、人間の行為がからむ社会現象、経済現象等と正規分布
自然現象、人間の行為がからむ社会現象、経済現象等の多くの現象は、分析すると、何故か正規分布に従うと統計学者は云う。
データをとって分析すると事実その分布に多くがなる。何故そうなるのかは、はっきりと分かっていない。
積算賃料、比準賃料も人間の行為に拠って求められた数値である。その数値より求められた倍率も人間の行為による現象の一つである事から、正規分布に従っているとする。
正規分布のグラフは、下記である。平均値を中心にして、左右対称の釣り鐘の形をしたグラフである。
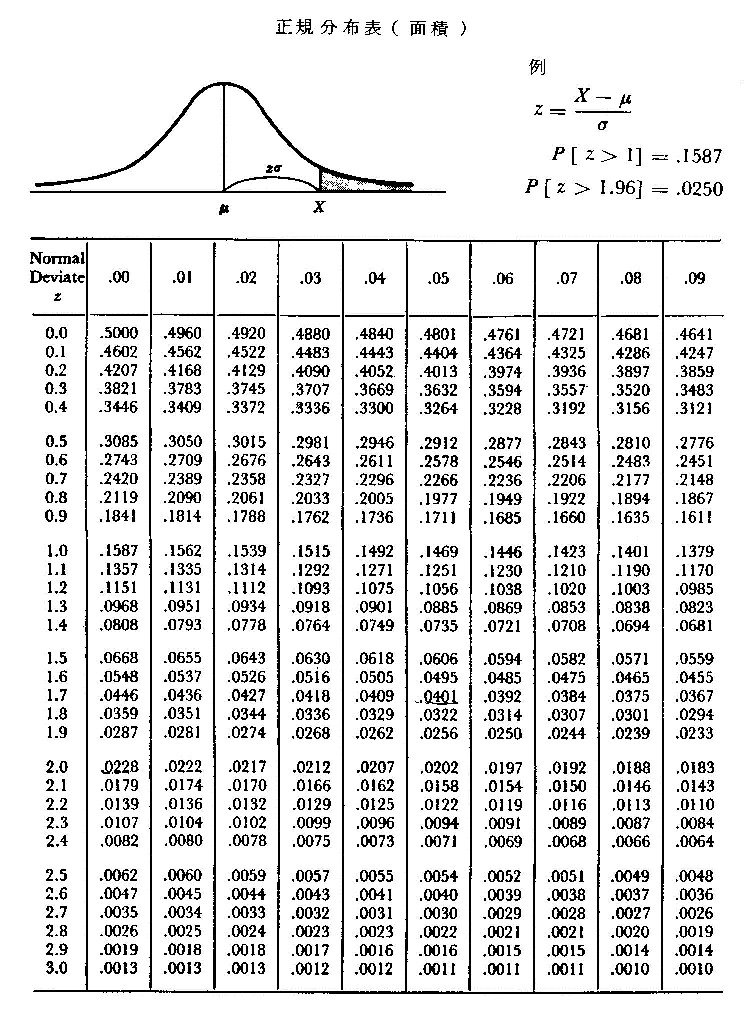
(山根太郎『統計学(上)』青学出版 P304 昭和51年3月)
8.Z値1.0の出現率は68.2%
① Z値
上記9判例、12事例の分析によって、平均は0.958であり、標準偏差は0.078と求められた。
正規分布のグラフは上図である。左右対称であるから、中心より右側のグラフで説明する。
グラフ右側半分の面積に対して、グラフ右端の裾野の黒塗りの面積の占める割合(分布率)が、Z値と呼ばれる面積割合であり、それが出現確率分布率となる。
データの平均をμ、標準偏差をσ、変数をXとすると、分布率Zは、
X-μ
Z=──────
σ
で求められる。
② Z値1.0のの分布率と出現率
イ、例題による説明
例えば、平均値0.958、標準偏差0.078のデータ結果があったとする。
X値が1.036であったとする。この1.036の数値以上のデータがどれ程あるのか求めるとする。
平均値μは0.958、標準偏差σは0.078、変数Xは1.036であるから、上記Z値の算式に代入する。
1.036-0.958
Z=─────────
0.078
0.078
=─────────
0.078
= 1.000
Z値は1.000と求められた。
前記の正規分布表の左側のZ値の縦欄の1.000を見ると、0.1587である。
Z値1.000の値となる割合は、15.87%ということである。1.010の場合は、その横の0.1562、即ち15.62%である。
これは右側半分のことであり、左半分も同じくある。
左右両方合わせて、
15.87%+15.87%=31.74%
31.74%以上あるということである。
このことを逆に考えると、上記正規分布グラフの黒塗りでない白い部分の割合は、
1-0.3174=0.6826
0.6826となる。白い部分の出現率は約68.2%である。
ロ、Z値1.0のの出現率
上記例題で使用した変数Xの1.036は、平均値0.958に、標準偏差0.078の1倍を加算した数値である。
0.958+0.078×1=1.036
それは正規分布グラフの右側の右隅の黒塗りの分布率である。
左右対称であるから、同様にグラフ左側の左隅の黒塗り(上図グラフには黒塗りがなされていないが、黒塗りされているものと考える。)の分布率は、
0.958-0.078×1=0.88
0.88である。
即ち、平均値に標準偏差の1倍を加減して求められた数値が、出現率68.2%の範囲と云うことになる。
出現率68.2%と云うことは、10回のうち7回出現するということにほぼなる。
9.一般的に許容されるZ値の数値は1.96である
世論調査、アンケート調査で有意水準ありとして統計学上許容されている調査数割合は5%である。片側グラフの分布率では、半分の2.5%と云うことになる。
上記正規分布表のZ値縦欄1.9の欄を右に向かい、1.96の個所の数値を見れば、0.0250とある。2.5%以上の分布が出るのはZ値1.96の値と云うことになる。
1.96以内であれば2.5%以下にならない、つまり5%以下にならないことから、統計学上有意水準があるとされ、世論調査結果、アンケート調査結果について信頼性が保てると云うことになる。
10.比準賃料/積算賃料の値が出現率5%以上の値
調査結果に信頼性が持てるのは、5%の出現率以上のデータ値ということである。
比準賃料/積算賃料の値にあっても、そのことが当てはまる。
裁判判例による比準賃料/積算賃料のデータ分析では、平均0.958、標準偏差0.078であった。
出現率5%の値が出るのはどこか。求める値をXとする。
Z値は1.96である。
正規分布表右側では、
X-0.958
1.96 =─────────
0.078
X=1.96×0.078+0.958
=1.110
1.110である。
正規分布表左側では、
0.958-X
1.96 =─────────
0.078
X=0.958 - 1.96×0.078
=0.805
0.805である。
出現率5%以上の比準賃料/積算賃料の値は、
0.805~1.110
の値である。
判決例の12データの求められたデータ値は、
0.836~1.054
である。
12データの求められたデータ値は、0.805~1.110内にあり、有意水準内にある事から、結果は信頼出来、妥当ということである。
新規賃料の比準賃料と積算賃料が妥当であると認められる賃料は、積算賃料に対して比準賃料が、
0.805~1.110
の間にある賃料の場合である。
この割合外にある場合の新規賃料は、出現率5%以下の賃料であり、統計学上の有意水準にあるとは云えず、妥当性ある新規賃料と認めることは困難であると云うことになる。
11. 比準賃料197,100円、積算賃料489,800円の妥当性の有無
① 妥当性の有無
比準賃料197,100円、積算賃料489,800円の積算賃料に対する比準賃料の倍率は
、
197,100円
─────── = 0.402
489,800円
である。
3つの価格及び賃料は理論上は一致すると云うが、実際には「資料不足」等で一致しない。
しかし、等価にならなく開差が生じるとしても、その開差にも限度がある。専門家の判断によるものであることから、その限度も大きく無いはずである。
比準賃料/積算賃料の倍率の妥当な倍率範囲は、上記分析から0.805~1.110と分析された。この倍率範囲が、開差の許容限度である。
上記0.402の倍率は、許容限度の倍率の範囲から大きく外れており、その倍率で求められている新規賃料は、統計学上の有意水準にあるとは認められず、信頼性が無いことになる。
② 比準賃料/積算賃料の0.402の出現率
比準賃料/積算賃料の倍率0.402の出現率を求めると、X値は0.402であるから、
0.958-0.402
Z =─────────
0.078
Z=7.12
7.12である。
エクセル計算によるZ値6.5~7.3までの分布表は、下記である。
|
Z値
|
0.000
|
0.010
|
0.020
|
0.030
|
0.040
|
0.050
|
|
6.5
|
4.03579E-11
|
3.77617E-11
|
3.5329E-11
|
3.30498E-11
|
3.09146E-11
|
2.89145E-11
|
|
6.6
|
2.06652E-11
|
1.9317E-11
|
1.80549E-11
|
1.68735E-11
|
1.57679E-11
|
1.47334E-11
|
|
6.7
|
1.04786E-11
|
9.78528E-12
|
9.13702E-12
|
8.53084E-12
|
7.96407E-12
|
7.43428E-12
|
|
6.8
|
5.26157E-12
|
4.90863E-12
|
4.57889E-12
|
4.27092E-12
|
3.98326E-12
|
3.7147E-12
|
|
6.9
|
2.61613E-12
|
2.43827E-12
|
2.27229E-12
|
2.11742E-12
|
1.97287E-12
|
1.83797E-12
|
|
7
|
1.28808E-12
|
1.19937E-12
|
1.11666E-12
|
1.0395E-12
|
9.67559E-13
|
9.00502E-13
|
|
7.1
|
6.28053E-13
|
5.84199E-13
|
5.43343E-13
|
5.05374E-13
|
4.69957E-13
|
4.36984E-13
|
|
7.2
|
3.03202E-13
|
2.81775E-13
|
2.61791E-13
|
2.4325E-13
|
2.2593E-13
|
2.09943E-13
|
|
7.3
|
1.44995E-13
|
1.34559E-13
|
1.249E-13
|
1.15907E-13
|
1.07581E-13
|
9.99201E-14
|
Z値7.12の正規分布値は、分布表によれば5.43E-13である。これは下記の値となる。
1
5.43×─────
1013
1
5.43×────────────────
10,000,000,000,000
10兆分の5.43の分布出現率である。
統計学上許容される出現率の割合は5%(5/100)以上である。
新規賃料が、比準賃料197,100円、積算賃料489,800円の分布出現率は10兆分の5.43(5.43/10,000,000,000,000)である、この様な出現率は統計学上から見て許容される割合では無い。
12.最後に
3つの価格・賃料は理論上は一致するが、実際においては、資料不足等で一致しない。一致しないと云っても、一致しない場合の価格差、賃料差の限度というものがあるハズである。
今迄それに付いて、研究、検討が全くなされていなかった。
今回、賃料評価における新規賃料を構成する積算賃料と比準賃料の間において、賃料増減額請求事件における判決に現れた新規賃料の積算賃料と比準賃料の分析によって、積算賃料と比準賃料の賃料開差の妥当な統計理論上の許容範囲がどれ程か知ることが出来た。
積算賃料に対して比準賃料の割合(比準賃料/積算賃料)を分析して、その割合は、
0.805~1.110
と分かった。
賃料評価において、新規賃料を求めるのに、積算賃料と比準賃料との間には上記割合が、経済合理性の経験則として存在している事を知って、不動産鑑定評価の専門家として適正な賃料鑑定評価に取り組んで欲しい。
以 上
鑑定コラム2422)「平澤春樹氏の「新規賃料の積算賃料と比準賃料の賃料額の関係について」のコラム紹介」
鑑定コラム2430)「ある借地権付建物の賃料評価の鑑定書」
鑑定コラム2579)「新規賃料の積算賃料と比準賃料の割合分析論文がEvaluation№76号に掲載」
▲
フレーム表示されていない場合はこちらへ
トップページ
前のページへ
次のページへ
鑑定コラム全目次へ
